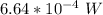Question

If 61.4 cm of copper wire (diameter = 1.08 mm, resistivity = 1.69 × 10-8Ω·m) is formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 9.14 mT/s, at what rate is thermal energy generated in the loop? Number Enter your answer in accordance to the question statement Units Choose the answer from the menu in accordance to the question statement

Answer 1

the thermal energy generated in the loop =
`6.64*10^(-4) \ W`

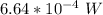
Step-by-step explanation:

Given that;

The length of the copper wire L = 0.614 m

Radius of the loop r =
`(L)/(2 \pi)`

r =
`(0.614)/(2 \pi)`

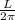
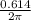
r = 0.0977 m

However , the area of the loop is :

`A_L = \pi r^2`

`A_L = \pi (0.0977)^2`

`A_L = 0.02999 \ m^2`

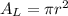
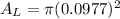
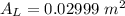
Change in the magnetic field is
`(dB)/(dt)= 0.0914 \ T/s`

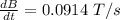
Then the induced emf e =
`A_L (dB)/(dt)`

e =
`0.02999 * 0.0914`

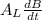
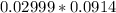
e = 2.74 × 10⁻³ V

resistivity of the copper wire
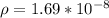`\rho = 1.69* 10^(-8)` Ω m

diameter of the wire = 1.08 mm

radius of the wire = 0.54 mm = 0.54 × 10⁻³ m

Thus, the resistance of the wire R =
`\frac {\rho L}{\pi r^2}`

R =
`((1.69*10^(-8))(0.614))/( \pi (0.54*10^(-3))^2)`

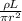
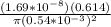
R = 1.13× 10⁻² Ω

Finally, the thermal energy generated in the loop (i.e the power) =
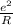
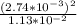
`(e^2)/(R)`

=
`((2.74*10^(-3))^2)/(1.13*10^(-2))`

=
`6.64*10^(-4) \ W`