Question

A supplier delivers an order for 20 electric toothbrushes to a store. By accident, three of the electric toothbrushes are defective. What is the probability that the first two electric toothbrushes sold are defective? Group of answer choices

Answer 1

The probability that the first two electric toothbrushes sold are defective is 0.016.

Explanation:

The probability of an event, say E occurring is:

`P (E)=(n(E))/(N)`

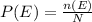
Here,

n (E) = favorable outcomes

N = total number of outcomes

Let X = number of defective electric toothbrushes sold.

The number of electric toothbrushes that were delivered to a store is, n = 20.

Number of defective electric toothbrushes is, x = 3.

The number of ways to select two toothbrushes to sell from the 20 toothbrushes is:

`{20\choose 2}=(20!)/(2!(20-2)!)=(20!)/(2!* 18!)=(20* 19* 18!)/(2!* 18!)=190`

The number of ways to select two defective toothbrushes to sell from the 3 defective toothbrushes is:

`{3\choose 2}=(3!)/(2!(3-2)!)=(3!)/(2!* 1!)=3`

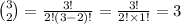
Compute the probability that the first two electric toothbrushes sold are defective as follows:

P (Selling 2 defective toothbrushes) = Favorable outcomes ÷ Total no. of outcomes

`=(3)/(190)\\`

`=0.01579\\\approx0.016`

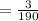
Thus, the probability that the first two electric toothbrushes sold are defective is 0.016.