Question

In Applied Life Data Analysis (Wiley, 1982), Wayne Nelson presents the breakdown time of an insulating fluid between electrodes at 34 kV. The times, in minutes, are as follows: 0.25, 0.82, 0.90, 1.21, 2.74, 3.23, 4.15, 4.72, 4.76, 6.40, 7.46, 7.94, 8.33, 12.09, 31.88, 32.47, 33.78, 36.77, and 72.78. Construct a normal probability plot of these data. Does it seem reasonable to assume that breakdown time is normally distributed? Choose the correct answer.

Answer 1

a) 14.3589 min

b) 18.8805 min

Explanation:

The mean is the sum of all values divided by the number of values:

x' = -0.19 + 0.78 + 0.96 + 1.31 + + 32.52 + 33.91 + 36.71 + 72.89/19

= 272.82/ 19

= 14.3589

n is the number of values in the data set.

n = 19

The variance is the sum of squared deviations from the mean divided by n — 1. The standard deviation is the square root of the variance:

s =
`√((0.19-14.3589)^2) +...+(72.89-14.3589)^2/19-1\\ = 18.8805`

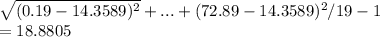
ALTERNATIVE METHOD FOR SAMPLE STANDARD DEVIATION

You can also determine the sample standard deviation using the formula:

formula is attached

Determine the two sums:

∑x_i = 0.19 + 0.78 + 0.96 + 1.31 + + 32.52 + 33.91 + 36.71 + 72.89 = 272.82

∑x_i^2 = 0.19^2 + 0.78^2 + 0.96^2 + 1.31^2 + 32.52^2 + 33.91^2 + 36.71^2 + 72.89^2 = 10333.8964

Using the formula with n = 19, we then obtain:

find the attachment

= 18.8805