Question

We want to create a 95% confidence interval to estimate the average yearly income of doctors who earned their degrees from public institutions. We sampled 40 doctors to obtain a mean of $145,580 and standard deviation of $13,200. 1) Do we use a t-value or a z-score? 2) Create a 95% confidence interval

Answer 1

1) use z-score

2) The 95% of confidence intervals

(141,489.24 , 149,670.75)

Explanation:

(i) we will use z-score

The 95% confidence interval for the mean of the population corresponding to the given sample.

`(x^(-) -z_(\alpha ) (S.D)/(√(n) ) ,x^(-) +z_(\alpha )(S.D)/(√(n) ) )`

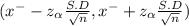
Given data the sample size n=40

mean of the sample x⁻ = $145,580

Standard deviation (σ) = $13,200

Level of significance z-score =1.96

ii) The 95% of confidence intervals

`(145,580-1.96((13200)/(√(40)) ) ,145580+1.96(13200)/(√(40) ) )`

on calculation, we get

(145,580-4090.75,145,580+4090.75)

(141,489.24 , 149,670.75)

Conclusion:-

The 95% of confidence intervals

(141,489.24 , 149,670.75)