Question

A bullet of mass 11 g strikes a ballistic pendulum of mass 1.9 kg. The center of mass of the pendulum rises a vertical distance of 10 cm. Assuming that the bullet remains embedded in the pendulum, calculate the bullet's initial speed.

Answer 1

The bullet's initial speed is 243.21 m/s.

Step-by-step explanation:

Given that,

Mass of the bullet,
`m_b=11\ g=0.011\ kg`

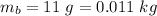
Mass of the pendulum,
`m_p=19\ kg`

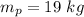
The center of mass of the pendulum rises a vertical distance of 10 cm.

We need to find the bullet's initial speed if it is assumed that the bullet remains embedded in the pendulum. Let it is v. In this case, the energy of the system remains conserved. The kinetic energy of the bullet gets converted to potential energy for the whole system. So,

`(1)/(2)(m_b+m_p)V^2 =(m_b+m_p)gh\\\\V=√(2gh) \ .................(1)`

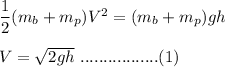
V is the speed of the bullet and pendulum at the time of collision

Now using conservation of momentum as :

`m_bv=(m_p+m_b)V`

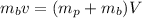
Put the value of V from equation (1) in above equation as :

`v=((m_p+m_b))/(m_b)√(2gh) \\\\v=((1.9+0.011))/(0.011)√(2* 9.8* 0.1)\\\\v=243.21\ m/s`

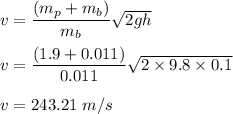
So, the bullet's initial speed is 243.21 m/s.