Question

At tequals​0, a train approaching a station begins decelerating from a speed of 160 ​mi/hr according to the acceleration function ​a(t)equalsnegative 1280 (1 plus 4 t )Superscript negative 3 ​mi/hrsquared​, where tgreater than or equals0. How far does the train travel between tequals0 and tequals0.2​? Between tequals0.2 and tequals0.4​?

Answer 1

The distance the train travels between 0 and 0.2 hours is 17.78 miles

The distance the train travels between 0.2 and 0.4 hours is 6.8376 miles

Explanation:

v₁ = 160 mi/hr at t = 0

Deceleration a = 1280 ( 1+ 4t)^(-3)

The velocity at a future time is given by

`v(t) = v(0)+\int\limits^t_0 a(t) \, dt`

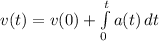
Therefore, plugging the values we get

`v(t) =160+\int\limits^t_0 -1280(1+4t)^(-3) \, dt`

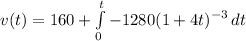
Which gives

`v(t) =160(1+4t)^(-2)`

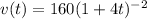
Similarly, the position of the vehicle is given by

`s(t) = s(0)+\int\limits^t_0 v(t) \, dt`

Which gives s(0) = 0 and
`v(t) =160(1+4t)^(-2)`

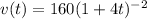
Therefore,

`s(t) = 0+\int\limits^t_0 160(1+4t)^(-2)\, dt`

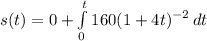
Which gives

`s(t) = (160t)/(4t+1)`

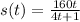
Therefore, the distance traveled between points 0 and 0.2 is given by

`s(0.2)-s(0) = (160* 0.2)/(4* 0.2+1) - 0 = 17.78 \, miles`

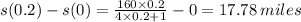
Similarly the distance the train travels between 0.2 and 0.4 seconds is

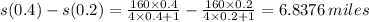`s(0.4)-s(0.2) = (160* 0.4)/(4* 0.4+1)-(160* 0.2)/(4* 0.2+1) = 6.8376 \, miles`.