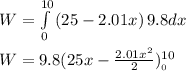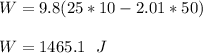Question

A 5 kg bucket is lifted from the ground into the air by pulling in 10 meters of rope with linear density of 2 kg/m at a constant speed. The bucket starts with 100 cm^3 of water and leaks at a constant rate. It finishes draining just as it reaches the 10 meter mark. How much work was spent lifting the bucket, rope, and water?

Answer 1

Workdone W = 1465.1 J

Step-by-step explanation:

The weight of the water = density × volume

weight of the water = 1000 kg/m³ × 100 cm³

weight of the water = 1000 kg/m³ × 0.0001 m³

weight of the water = 0.1 kg

weight of the bucket = 5 kg

weight of the rope =
`2*10- 2x\\\\`

=
`20- 2x`

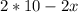
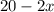
Leakage =
`(0.1)/(10) * x`

=
`0.01 x`

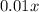
Total weight =
`5 + 20 - 2x - 0.01 x`

=
`25 - 2.01 x`

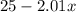
Force = wg

Force = (
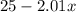`25 - 2.01 x`)g

Force = 9.8 (
`25 - 2.01 x`)

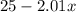Finally; the amount of work spent in lifting the bucket, rope, and water is calculated as follows:

`W = \int\limits^(10)_0 {(25-2.01 x)} \, 9.8 dx \\\\W = 9.8 (25x - (2.01x^2)/(2)})^(10)__0\\\\`

`W = 9.8 (25*10-2.01*50)\\\\W = 1465.1 \ \ J`