Question

A converging-diverging nozzle is designed to operate with an exit Mach number of 1.75 . The nozzle is supplied from an air reservoir at 5 MPa. Assuming one-dimensional flow, calculate the following: a. Maximum back pressure to choke the nozzle. b. Range of back pressures over which a normal shock will appear in the nozzle. c. Back pressure for the nozzle to be perfectly expanded to the design Mach number. d. Range of back pressures for supersonic flow at the nozzle exit plane.

Answer 1

a. 4.279 MPa

b. 3.198 MPa to 4.279 MPa

c. 0.939 MPa

d. Below 3.198 MPa

Step-by-step explanation:

From the given parameters

M
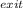`_(exit)` = 1.75 MPa

M at 1.6 MPa gives A
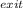`_(exit)`/A* = 1.2502

M at 1.8 MPa gives A
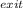`_(exit)`/A* = 1.4390

Therefore, by interpolation, we have M
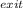`_(exit)` = 1.75 MPa gives A

However, we shall use M
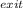`_(exit)` = 1.75 MPa and A

Similarly,

P
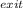`_(exit)`/P₀ = 0.1878

a) Where the nozzle is choked at the throat there is subsonic flow in the following diverging part of the nozzle. From tables, we have

A
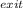`_(exit)`/A* = 1.387. by interpolation M

Therefore P
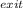`_(exit)` = P₀ × P

Which shows that the nozzle is choked for back pressures lower than 4.279 MPa

b) Where there is a normal shock at the exit of the nozzle, we have;

M₁ = 1.75 MPa, P₁ = 0.1878 × 5 = 0.939 MPa

Where the normal shock is at M₁ = 1.75 MPa, P₂/P₁ = 3.406

Where the normal shock occurs at the nozzle exit, we have

`P_b = 3.406* 0.939 = 3.198 MPa`

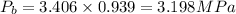
Where the shock occurs t the section prior to the nozzle exit from the throat, the back pressure was derived as
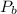`P_b` = 4.279 MPa

Therefore the back pressure value ranges from 3.198 MPa to 4.279 MPa

c) At M
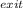`_(exit)` = 1.75 MPa and P

d) Where the back pressure is less than 3.198 MPa according to isentropic flow relations supersonic flow will exist at the exit plane