Question

Suppose a random sample of size 50 is selected from a population with . Find the value of the standard error of the mean in each of the following cases (use the finite population correction factor if appropriate). The population size is infinite. The population size is . The population size is . The population size is .

Answer 1

(a) The standard error of the mean when the population size is N = ∞ is 1.4142.

(b) The standard error of the mean when the population size is N = 50000 is 1.414.

(c) The standard error of the mean when the population size is N = 5000 is 1.4073.

(d) The standard error of the mean when the population size is N = 500 is 1.3430.

Explanation:

The question is:

Suppose a simple random sample of size 50 is selected from a population with σ = 10. Find the value of the standard error of the mean in each of the following cases (use the finite population correction factor if appropriate).

a. The population size is infinite.

b. The population size is N = 50,000.

c. The population size is N = 5000.

d. The population size is N = 500.

Then the formula for standard error of sample means using the fpc (finite population correction) factor is given by,

`SE_(fpc)=(\sigma)/(√(n))*\sqrt{(N-n)/(N-1)`

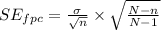
(a)

Compute the standard error of the mean when the population size is N = ∞ and sample size n = 50 as follows:

`SE_(fpc)=(\sigma)/(√(n))*\sqrt{(N-n)/(N-1)`

`SE_(fpc)=(\sigma)/(√(n))`

`=(10)/(√(50))`

`=1.4142`

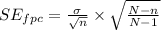
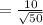
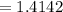
Thus, the standard error of the mean when the population size is N = ∞ is 1.4142.

(b)

Compute the standard error of the mean when the population size is N = 50000 and sample size n = 50 as follows:

`SE_(fpc)=(\sigma)/(√(n))*\sqrt{(N-n)/(N-1)`

`=(10)/(√(50))*\sqrt{(50000-50)/(50000-1)`

`=1.4135`

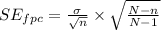
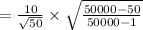
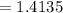
Thus, the standard error of the mean when the population size is N = 50000 is 1.414.

(c)

Compute the standard error of the mean when the population size is N = 5000 and sample size n = 50 as follows:

`SE_(fpc)=(\sigma)/(√(n))*\sqrt{(N-n)/(N-1)`

`=(10)/(√(50))*\sqrt{(5000-50)/(5000-1)`

`=1.4073`

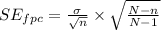
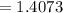
Thus, the standard error of the mean when the population size is N = 5000 is 1.4073.

(d)

Compute the standard error of the mean when the population size is N = 500 and sample size n = 50 as follows:

`SE_(fpc)=(\sigma)/(√(n))*\sqrt{(N-n)/(N-1)`

`=(10)/(√(50))*\sqrt{(500-50)/(500-1)`

`=1.3430`

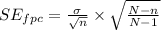
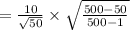
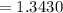
Thus, the standard error of the mean when the population size is N = 500 is 1.3430.