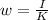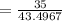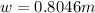Question

Point PP is a distance d1d1 = 4.0 mm above a large sheet of metal that carries a current of 35 AA in the positive xx direction and a distance d2d2 = 3.0 mm below a very long wire that carries a current of 0.41 AA in the positive xx direction. If the magnetic field magnitude at P is zero, calculate the width of the metal sheet.

Answer 1

The width of the sheet is
`w =0.8046m`

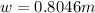
Step-by-step explanation:

From the question we are told that

The distance of point P above a large sheet of metal is
`D = 4.0mm =(4)/(1000) = 0.004m`

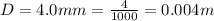
The current on the large metal sheet is
`I =34A`

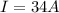
The distance of the the point P below a long wire
`d = 3.0mm = (3)/(1000) = 0.003m`

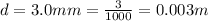
The current on the long wire is
`I_w = 0.41A`

The magnetic field at P is
`B = 0T`

Generally magnetic field of P long wire is mathematically represented as

`B_w = (\mu_o I_w)/(2\pi r)`

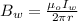
Generally magnetic field of P large sheet of meta is mathematically represented as

`B_m = (\mu_o K)/(2)`

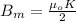
Where K is the current per unit width

The total magnetic field at P is

`(\mu_o I_w)/(2 \pi r) = (\mu_o K)/(2)`

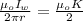
Making K the subject of formula

`K = (2 I_w )/(2 \pi r )`

Substituting values

`K = (2 * 0.41 )/(2 * 3.142 * (0.0030) )`

`K = 43.4967 A/m`

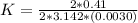
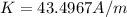
Generally K is mathematically represented as

`K = (I)/(w)`

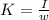
Where w is the width of the large sheet

Therefore the width of the metal sheet
`w = (I)/(K)`

`= (35)/(43.4967)`

`w =0.8046m`