Question

drug sniffing dogs must be 95% accurate in their responses because their handlers don't want them to miss durgs and also don't want false positives. a new dog is being tested and is right in 46 of 50 trials. find the 95% confidence interval for the proportion of times the dog will be correct

Answer 1

95% Confidence interval: (0.8449,0.9951)

Explanation:

We are given the following in the question:

Sample size, n = 50

Number of times the dog is right, x = 46

`\hat{p} = (x)/(n) = (46)/(50) = 0.92`

95% Confidence interval:

`\hat{p}\pm z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

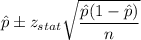
Putting the values, we get:

`0.92 \pm 1.96(\sqrt{(0.92(1-0.92))/(50)})\\\\ = 0.92\pm 0.0751\\\\=(0.8449,0.9951)`

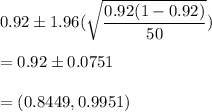
(0.8449,0.9951) is the required 95% confidence interval for the proportion of times the dog will be correct.