Answer:
Therefore x=9
Explanation:
Give that,
log x+ log (x-3) = log 54
log x(x-3) =log 54 [
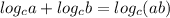 ]
]
x(x-3) = 54
Now expand the above equation to get a quadratic equation
x²-3x=54
⇒x²-9x+6x-54=0
⇒x(x-9)+6(x-9)=0
⇒(x-9)(x+6)=0
⇒x-9=0 or, x+6=0
⇒x=9,-6
Now putting x= -6 in the given expression,
log(-6)+log(-6-9)=log 54.
Since log (-6) does not exist.
Therefore x=9