Question

A limited edition poster increases in value each year with an initial value of $18. After one year and an increase of 15% per year, the poster is worth $20.70. Which equation can be used to fund the value, y, after x years?

Answer 1

We have been given that a limited edition poster increases in value each year with an initial value of $18. After one year and an increase of 15% per year, the poster is worth $20.70.

We will use exponential growth formula to find our required equation.

We know that an exponential function is in form
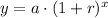`y=a\cdot (1+r)^x`, where

a = Initial value,

r = Growth rate in decimal form,

x = Time.

Let us convert 15% into percentage.

`15\%=(15)/(100)=0.15`

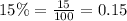
Initial value is 18.

Upon substituting these values in above formula, we will get:

`y=18(1+0.15)^x`

`y=18(1.15)^x`

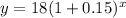
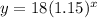
Let us check our function by finding the value of poster after one year as:

`y=18(1.15)^1`

`y=18(1.15)`

`y=20.70`

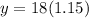
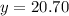
Since the value of poster after 1 year matched with our findings, therefore, the equation
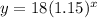`y=18(1.15)^x`can be used to fund the value, y, after x years.