Question

Find the temperature at which Kp = 42.0 for the reaction

H2(g) + I2(g) → 2HI(g)

[Given: at 25°C, for H2(g), ∆H°f = 0, S° = 131.0 J/mol·K; for I2(g), ∆H°f = 62.26 kJ/mol, S° = 260.6 J/mol·K; for HI(g), ∆H°f = 25.9 kJ/mol, S° = 206.3 J/mol·K; assume that ∆H° and ∆S° are independent of temperature.]

Answer 1

Answer: Temperature for the given reaction is 1040 K (approx).

Step-by-step explanation:

Formula for enthalpy change of a reaction is as follows.

`\Delta H_(rxn) = \Delta H_(products) - \Delta H_(reactants)`

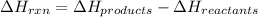
For the given reaction equation,

`\Delta H_(rxn) = 2 * \Delta H_(HI) - (\Delta H_{H_(2)} + \Delta H_{I_(2)})`

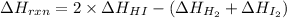
Now, putting the given values into the above formula as follows.

`\Delta H_(rxn) = 2 * \Delta H_(HI) - (\Delta H_{H_(2)} + \Delta H_{I_(2)})`

`\Delta H_(rxn) = 2 * 25.9 - (0 + 62.26)`

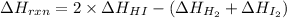
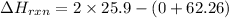
= -10460 J/mol

Now, we will calculate the change in its entropy as follows.

`\Delta S = S_(products) - S_(reactants)`

=
`2 * S_(HI) - (S_{H_(2)} + S_{I_(2)})`

=
`2 * 206.3 - (131.0 + 260.6)`

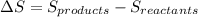
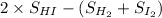
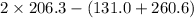
= 21 J/mol

Also, we know that

`\Delta G = RT ln K_(p) = \Delta H_(rxn) - T\Delta S_(rxn)`

`-8.314 * T * ln(42) = -10460 - T * 21`

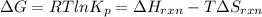
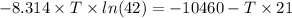
T = 1036.7 K

= 1040 K

Therefore, we can conclude that temperature for the given reaction is 1040 K (approx).