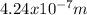Answer:
Speed:
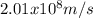
Wavelength:
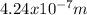
Frequency:
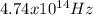
Step-by-step explanation:
The speed of the laser as it travels through polystyrene can be determine by means of the equation of the refraction index:
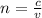 (1)
(1)
Where c is the speed of light and v is the speed of the laser in the medium.
Therefore, v will be isolated from equation 1
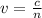
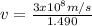
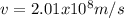
Hence, the speed of the laser has a value of
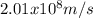
Frenquency:
Since, wavelength is the only one who depends on the media. Therefore the frequency in both medium will be the same.
To determine the frequency it can be used the following equation
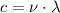 (2)
(2)
Where c is the speed of light,
 is the frequency and
is the frequency and
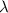 is the wavelength
is the wavelength
Then,
 wil be isolated from equation 2.
wil be isolated from equation 2.
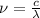 (3)
(3)
Before using equation 3 it is necessary to express
 in units of meters.
in units of meters.
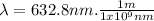 ⇒
⇒
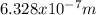
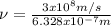
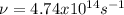
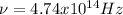
Hence, the frequency of the laser has a value of
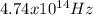
Wavelength:
To determine the wavelength it can be used:
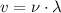
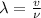
Where v is the speed of the laser through the polystyrene.
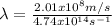
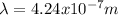
Hence, the wavelength of the laser has a value of