Answer:
There are a total of 23 cars with air conditioning and automatic transmission but not power steering
Explanation:
Let A be the cars that have Air conditioning, B the cars that have Automatic transmission and C the cars that have pwoer Steering. Lets denote |D| the cardinality of a set D.
Remember that for 2 sets E and F, we have that
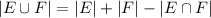
Also,
|E| = |E ∩F| + |E∩F^c|
We now alredy the following:
|A| = 89
|B| = 99
|C| = 74

|(A \cup B \cup C)^c| = 24
|A \ (B U C)| = 24 (This is A minus B and C, in other words, cars that only have Air conditioning).
|B \ (AUC)| = 65
|C \ (AUB)| = 26
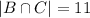
We want to know |(A∩B) \ C|. Lets calculate it by taking the information given and deducting more things
For example:
99 = |B| = |B ∩ C| + |B∩C^c| = 11 + |B∩C^c|
Therefore, |B∩C^c| = 99-11 = 88
And |A ∩ B ∩ C^c| = |B∩C^c| - |B∩C^c∩A^c| = |B∩C^c| - |B \ (AUC)| = 88-65 = 23.
This means that the amount of cars that have both transmission and air conditioning but now power steering is 23.