Question

A golfer keeps track of his score for playing nine holes of golf​ (half a normal golf​ round). His mean score is 8080 with a standard deviation of 1313. Assuming that the second 9 has the same mean and standard​ deviation, what are the mean and standard deviation of his total score if he plays a full 18​ holes?

Answer 1

Therefore the mean and standard deviation of his total score if he plays a full 18 holes are 160 and
`11\sqrt2` respectively.

Explanation:

Given that,

For the first 9 holes X:

E(X) = 80

SD(X)=13

For the second 9 holes Y:

E(Y) = 80

SD(Y)=13

For the sum W=X+Y, the following properties holds for means , variance and standard deviation :

E(W)=E(X)+E(Y)

and

V(W)=V(X)+V(Y)

⇒SD²(W)=SD²(X)+SD²(Y) [ Variance = (standard deviation)²]

`\Rightarrow SD(W)=√(SD^2(X)+SD^2(Y))`

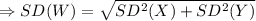
∴E(W)=E(X)+E(Y) = 80 +80=160

and

∴
`SD(W)=√(SD^2(X)+SD^2(Y))`

`=√(11^2+11^2)`

`=√(2.11^2)`

`=11\sqrt2`

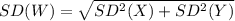
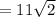
Therefore the mean and standard deviation of his total score if he plays a full 18 holes are 160 and
`11\sqrt2` respectively.