Question

Consider two securities, A and B. Securities A and B have a correlation coefficient of 0.35. Security A has standard deviation of 12%, and security B has standard deviation of 25%. Calculate the covariance between these two securities.

Answer 1

The co-variance between these two securities is 0.0105

Explanation:

We are given the following in the question:

Correlation coefficient = 0.35

`Corr(A,B) = 0.35`

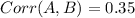
Standard deviation of Security A = 12%

`\sigma_(A) = 0.12`

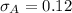
Standard deviation of Security B = 25%

`\sigma_(B) = 0.25`

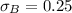
We have to find the co-variance between these two securities.

Formula:

`Corr(A,B) =(Cov(A,B))/(\sigma_A* \sigma_B)`

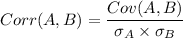
Putting values, we get,

`0.35 = (Cov(A,B))/(0.12* 0.25)\\\\Cov(A,B) = 0.35* 0.12 * 0.25=0.0105`

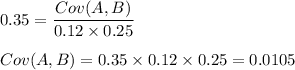
Thus, the co-variance between these two securities is 0.0105