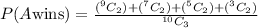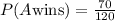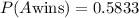Question

An urn contains 3 red and 7 black balls. Players A and B take turns (A goes first) withdrawing balls from the urn consecutively. What is the probability that A selects the first red ball? Express your answer as a decimal rounded to the next hundredth, e.g. 0.24 for 0.23932

Answer 1

The probability that A selects the first red ball is 0.5833.

Explanation:

Given : An urn contains 3 red and 7 black balls. Players A and B take turns (A goes first) withdrawing balls from the urn consecutively.

To find : What is the probability that A selects the first red ball?

Solution :

A wins if the first red ball is drawn 1st,3rd,5th or 7th.

A red ball drawn first, there are
`E(1)= ^9C_2` places in which the other 2 red balls can be placed.

A red ball drawn third, there are
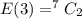`E(3)= ^7C_2` places in which the other 2 red balls can be placed.

A red ball drawn fifth, there are
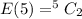`E(5)= ^5C_2` places in which the other 2 red balls can be placed.

A red ball drawn seventh, there are
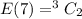`E(7)= ^3C_2` places in which the other 2 red balls can be placed.

The total number of total event is
`S= ^(10)C_3`

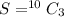
The probability that A selects the first red ball is

`P(A \text{wins})=((^9C_2)+(^7C_2)+(^5C_2)+(^3C_2))/(^(10)C_3)`

`P(A \text{wins})=(36+21+10+3)/(120)`

`P(A \text{wins})=(70)/(120)`

`P(A \text{wins})=0.5833`