Answer:
487.23 N/m
Step-by-step explanation:
Given:
mass of metal sphere 'm'= 0.51kg
the spring stretches from 0.12 m to 0.23 m. Therefore,
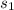 = 0.12m and
= 0.12m and
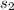 = 0.23m
= 0.23m
the speed of the sphere decreases from 6.7 to 3.3 m/s. Therefore,
 = 6.7m/s and
= 6.7m/s and
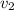 =3.3m/s
=3.3m/s
In order to find spring constant, we apply law of conservation of energy. i.e
The change of the kinetic energy of sphere is equal to the change of potential energy of the spring.
So, Δ
 Δ
Δ
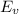
where,
Δ
 1/2 m (
1/2 m (
 -
-
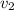 )²
)²
Δ
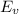 = 1/2 k (
= 1/2 k (
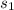 -
-
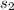 )²
)²
1/2 m (
 -
-
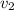 )² = 1/2 k (
)² = 1/2 k (
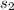 -
-
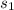 )²
)²
k= m [ (
 -
-
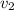 )²/(
)²/(
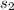 -
-
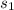 )²
)²
k= 0.51 [(6.7-3.3)²/ (0.23-0.12)²]
k= 487.23 N/m
Thus, the spring constant of the spring is 487.23 N/m