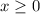Question

(a) The parametric equations x = f(t) and y = g(t) give the coordinates of a point (x, y) = (f(t), g(t)) for appropriate values of t. The variable t is called ___________ .

(b) Suppose that the parametric equations x = t, y = t^2, t >_ 0, model the position of a moving object at time t. When t = 0, the object is at __________ and when t = 6, the object is at ___________.
(c) If we eliminate the parameter in part (b), we get the equation ____________.

Answer 1

Answer:.....................................

Answer 2

Explanation:

a). Given a parametric equation, we are describing a set of coordinates based on the value of t. The variable t is called the parameter.

b) we have the following equations. x=t y=t^2, so in order for us to know where the object is at t=t' we must replace t with the specific value t'. Hence, when t=0 the object is at (0,0^2) = (0,0) (the origin). When t=6, the object is at (6,6^2) = (6,36).

c). To eliminate the parameter, we replace the parameter in one equation by using the second equation. Recall that we have that x=t. Then, by replacing in the second equation, we have the following

`y=t^2 = (x)^2 = x^2`

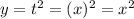
where
`x\geq 0`