Question

NASA is conducting an experiment to find out the fraction of people who black out at G forces greater than 6. In an earlier study, the population proportion was estimated to be 0.36. How large a sample would be required in order to estimate the fraction of people who black out at 6 or more Gs at the 85% confidence level with an error of at most 0.04? Round your answer up to the next integer.

Answer 1

The large sample n = 190.44≅190

The large sample would be required in order to estimate the fraction of people who black out at 6 or more Gs at the 85% confidence level with an error of at most 0.04 is n = 190.44

Explanation:

Given population proportion was estimated to be 0.3

p = 0.3

Given maximum of error E = 0.04

we know that maximum error

`M.E = (Z_(\alpha ) √(p(1-p)) )/(√(n) )`

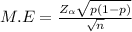
The 85% confidence level
`z_(\alpha ) = 1.44`

`√(n) = (Z_(\alpha ) √(p(1-p)) )/(m.E)`

`√(n) = (1.44X√(0.3(1-0.3) )/(0.04)`

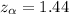
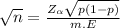
now calculation , we get

√n=13.80

now squaring on both sides n = 190.44

large sample n = 190.44≅190

Conclusion:-

Hence The large sample would be required in order to estimate the fraction of people who black out at 6 or more Gs at the 85% confidence level with an error of at most 0.04 is n = 190.44