Question

The volume V (in cubic centimeters) of 1 kg of water at a temperature T, where T is between 0 ◦C and 30◦C, is given approximately by the formula V = 999.87 − 0.06426T + 0.0085043T 2 − 0.0000679T 3 . Find the temperature at which water has its maximum density on this interval.

Answer 1

Therefore water has its maximum density at 3.97°C.

Explanation:

Given that,

The volume of 1 kg of water at a temperature T is

V=999.87-0.06426T+0.0085043T²-0.0000679T³

where T is between 0°C and 30°C.

We know,

Density = Volume ÷ mass.

Here mass = 1 kg.

⇒Density = Volume ÷ 1 kg

⇒Density = Volume

Therefore the density of the water will be maximum only when the volume of the water is maximum.

V=999.87-0.06426T+0.0085043T²-0.0000679T³

Differentiating with respect T

V'= -0.06426+0.0170086T-0.0002037T²

Again differentiating with respect T

V''=0.0170086-0.0004074T

For the maximum value volume , V'=0

-0.06426+0.0170086T-0.0002037T²=0

⇒ 0.06426-0.0170086T+0.0002037T²=0

[ Applying quadratic formula
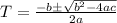`T=(-b\pm√(b^2-4ac))/(2a)` , here a=0.0002037, b =-0.0170086 and c =0.06426]

∴T=3.97, 79.53

Since the value of T is between 0°C and 30°C,

So, T=3.97°C

Therefore at T=3.97°C, the volume is maximum.

It means the density of the water will be maximum at 3.97°C.

Therefore water has its maximum density at 3.97°C.