Question

Refrigerant-134a enters the coils of the evaporator of a refrigeration system as a saturated liquid–vapor mixture at a pressure of 140 kPa. The refrigerant absorbs 180 kJ of heat from the cooled space, which is maintained at -10oC, and leaves as saturated vapor at the same pressure. Determine (a) the entropy change of the refrigerant, (b) the entropy change of the cooled space, and (c) the total entropy change for this process.

Answer 1

(a). Entropy change of refrigerant is = 0.7077
`(KJ)/(K)`

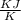
(b). Entropy change of cooled space
`dS_(space) = - 0.6844`
`(KJ)/(K)`

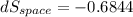
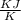
(c). Total entropy change is dS = 0.0232
`(KJ)/(K)`

Step-by-step explanation:

Given data

Saturation pressure = 140 K pa

Saturation temperature from property table

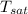`T_(sat)` = - 18.77 °c = - 18.77 + 273 = 254.23 K

(a). Entropy change of refrigerant is given by

`dS_(ref) = (Q)/(T_(sat))`

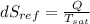
Since heat absorbed by refrigerant Q = 180 KJ

`dS = (180)/(254.23)`

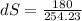
dS = 0.7077
`(KJ)/(K)`

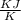
(b). Entropy change of cooled space

`dS_(space) = - (Q)/(T_(space))`

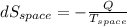
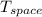`T_(space)` = - 10 °c = 263 K

`dS_(space) = - (180)/(263)`

`dS_(space) = - 0.6844`
`(KJ)/(K)`

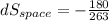
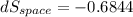
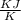
(c). Total entropy change is given by

`dS = dS_(ref) + dS_(space)`

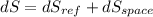
dS = 0.7077 - 0.6844

dS = 0.0232
`(KJ)/(K)`

This is the value of total entropy change.