Question

A fair die is cast, a fair coin is tossed, and a card is drawn from a standard deck of 52 playing cards. Assuming these events are independent, what is the probability that the number falling on the uppermost part of the die is a 6, the coin shows a head, and the card drawn is a face card? (Round your answer to 4 decimal places.)

Answer 1

0.0192 (Correct to 4 decimal places)

Explanation:

For the Fair Die

Sample Space ={1,2,3,4,5,6}

n(S)=6

• P(The uppermost part of the die is a 6),
  `P(A) =(1)/(6)`

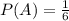
For the Coin

Sample Space ={Head, Tail}

n(S)=2

• P(The coin shows a head),
  `P(B) =(1)/(2)`

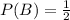
For the Card

n(S)=52 Cards

So, there are 13 cards of each suit. Among these 13 cards, there are 3 picture cards or face cards as they are called. These are the Jack, Queen and King cards.

Number of Picture Cards =12

• P(The card drawn is a picture card),
  `P(C) =(12)/(52)`

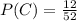
Since the events are independent,

`P(A \cap B \cap C)=P(A) \cdot P(B) \cdot P(C)`

`=(1)/(6)X (1)/(2)X(12)/(52)\\=0.0192`

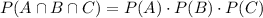
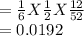
Therefore, the probability that the number falling on the uppermost part of the die is a 6, the coin shows a head, and the card drawn is a face card is 0.0192 (Correct to 4 decimal places).

Answer 2

The probability is 0.0192 to four decimal places.

Explanation:

In this question, we are asked to calculate the probabilities that three events will occur at the same time.

Firstly, we identify the individual probabilities.

The probability of 6 showing In a throw of die is 1/6

The probability of a coin showing head in a flip of coin is 1/2

The probability of a face card being drawn in a deck of cards is 12/52( There are 12 face cards in a deck of cards)

Mathematically to get the probability of all these events happening, we simply multiply all together.

This will be ;

1/6 * 1/2 * 12/52 = 1/52 = 0.0192 ( to 4 decimal place)