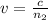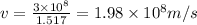Question

A laser beam is incident at an angle of 30.0° from the vertical onto a solution of corn syrup in water. The beam is refracted to 19.24° from the vertical. (a) What is the index of refraction of the corn syrup solution? Assume that the light is red, with vacuum wavelength 632.8 nm. Find its (b) wavelength, (c) frequency, and (d) speed in the solution.

Answer 1

Answer with Explanation:

We are given that

Angle of incidence,
`i=30^(\circ)`

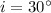
Angle of refraction,
`r=19.24^(\circ)`

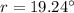
a.Refractive index of air,
`n_1=1`

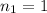
We know that

`n_2sinr=n_1sini`

`n_2=(n_1sin i)/(sin r)=(sin30)/(sin19.24)=1.517`

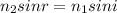
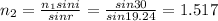
b.Wavelength of red light in vacuum,
`\lambda=632.8nm=632.8* 10^(-9) m`

`1nm=10^(-9) m`

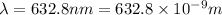
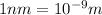
Wavelength in the solution,
`\lambda'=(\lambda)/(n_2)`

`\lambda'=(632.8)/(1.517)=417nm`

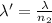
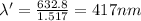
c.Frequency does not change .It remains same in vacuum and solution.

Frequency,
`\\u=(c)/(\lamda)=(3* 10^8)/(632.8* 10^(-9))`

Where
`c=3* 10^8 m/s`

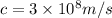
Frequency,
`\\u=4.74* 10^(14)Hz`

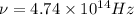
d.Speed in the solution,
`v=(c)/(n_2)`

`v=(3* 10^8)/(1.517)=1.98* 10^8m/s`