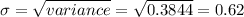Question

You play two games against the same opponent. The probability you win the first game is 0.4. If you win the first game, the probability you also win the second one is 0.2. If you lose the first game, the probability that you win the second game is 0.3.

a. Are the two games independent?
Explain your answer.
b. What's the probability you lose both games?
c. What's the probability you win both games?
d. Let random variable X be the number of games you win. Find the probability model for X complete the table below (hint: use your answers in part b and c)
X P(x)
0
1
2
e. Find and interpret the expected value of X?
f. What is the standard deviation of X?

Answer 1

a) No

b) 42%

c) 8%

d) X 0 1 2

P(X) 42% 50% 8%

e) 0.62

Explanation:

a) No, the two games are not independent because the the probability you win the second game is dependent on the probability that you win or lose the second game.

b) P(lose first game) = 1 - P(win first game) = 1 - 0.4 = 0.6

P(lose second game) = 1 - P(win second game) = 1 - 0.3 = 0.7

P(lose both games) = P(lose first game) × P(lose second game) = 0.6 × 0.7 = 0.42 = 42%

c) P(win first game) = 0.4

P(win second game) = 0.2

P(win both games) = P(win first game) × P(win second game) = 0.4 × 0.2 = 0.08 = 8%

d) X 0 1 2

P(X) 42% 50% 8%

P(X = 0) = P(lose both games) = P(lose first game) × P(lose second game) = 0.6 × 0.7 = 0.42 = 42%

P(X = 1) = [ P(lose first game) × P(win second game)] + [ P(win first game) × P(lose second game)] = ( 0.6 × 0.3) + (0.4 × 0.8) = 0.18 + 0.32 = 0.5 = 50%

e) The expected value
`\mu=\Sigma}xP(x)= (0*0.42)+(1*0.5)+(2*0.08)=0.66`

f) Variance
`\sigma^2=\Sigma(x-\mu^2)p(x)= (0-0.66)^2*0.42+ (1-0.66)^2*0.5+ (2-0.66)^2*0.08=0.3844`

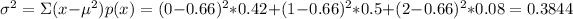
Standard deviation
`\sigma=√(variance) = √(0.3844)=0.62`