Question

Interactive LearningWare 8.1 reviews the approach that is necessary for solving problems such as this one. A motorcyclist is traveling along a road and accelerates for 4.36 s to pass another cyclist. The angular acceleration of each wheel is 6.10 rad/s2, and, just after passing, the angular velocity of each is 75.2 rad/s, where the plus signs indicate counterclockwise directions. What is the angular displacement of each wheel during this time?

Answer 1

The angular displacement of each wheel is 269.92 rad

Step-by-step explanation:

Given:

Angular acceleration
`\alpha = 6.10 (rad)/(s^(2) )`

Time to pass cyclist
`t = 4.36` s

Angular velocity
`\omega _(f) = 75.2 (rad)/(s)`

According to the equation of kinematics,

`\omega _(f) = \omega _(i) + \alpha t`

`\omega _(i) = \omega _(f) - \alpha t`

`\omega _(i) = 75.2 - 6.10 * 4.36`

`\omega _(f) = 48.60`
`(rad)/(s)`

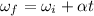
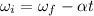
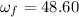
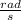
For finding angular displacement,

`\omega _(f) ^(2) - \omega _(i) ^(2) = 2 \alpha \theta`

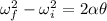
Where
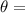`\theta =` angular displacement,

`\theta = (\omega _(f)^(2) - \omega _(i) ^(2) )/(2\alpha )`

`\theta = (5655.04 - 2361.96 )/(2* 6.10 )`

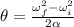
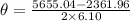
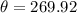`\theta = 269.92` rad

Therefore, the angular displacement of each wheel is 269.92 rad