Question

Find the value of x at which the function has a possible relative maximum or minimum point.​ (Recall that e Superscript x is positive for all​ x.) Use the second derivative to determine the nature of the function at these points.

f(x)=(3+x)e-4x

What is the value of x at which the function has a possible relative maximum or minimum point?

1a. Is the point a relative maximum or mininum?

Answer 1

x= -11/4 is a maximum.

Explanation:

Remember that a function has its critical points where the derivative equal zero. Therefore we need to compute the derivative of this function and find the points where the derivative is zero. Using the chain rule and the product rule we get that

`f'(x)= -e^(-4x)(11+4x)`

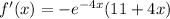
And then we get that if
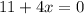`11+4x = 0` then
`x = -11/4` . So it has a critical point at
`x = -11/4`.

Now, if the second derivative evaluated at that point is less than 0 then the point is a maximum and if is greater than zero the point is a minimum.

Since

`f''(x) = 8e^(-4x) (5+2x)\\f''(-11/4) = -239496.56`

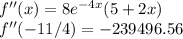
x= -11/4 is a maximum.