Question

A water tank has the shape of an inverted circular cone (vertex points downward). The height of the tank is 400 cm and its radius is 100cm. Water is leaking from the tank at a rate of 250cm3 per hour. At what rate is the height of the water in the tank changing when the height is 300cm

Answer 1

We have been given that a water tank has the shape of an inverted circular cone (vertex points downward). The height of the tank is 400 cm and its radius is 100 cm. Water is leaking from the tank at a rate of 250 cm^3 per hour.

We are asked to find the rate at which height of water in the tank is changing, when the height is 300 cm.

We will use volume of cone formula to solve our given problem.

`V=(1)/(3)\pi r^2 h`, where,

r = Radius of cone,

h = Height of cone.

Our next step is to write our volume in terms of height. We have been given a relation between height and radius as:

`(r)/(h)=(100)/(400)`

`(r)/(h)=(1)/(4)`

`r=(1)/(4)h`

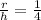
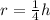
Upon substituting this value in volume formula, we will get:

`V=(1)/(3)\pi((1)/(4)h)^2 h`

`V=(1)/(3)\pi((h^2)/(16)) h`

`V=(1)/(3)\pi\cdot (h^3)/(16)`

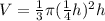
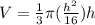
Now we will take the derivative of volume with respect to time as:

`(dV)/(dt)=(1)/(3)\pi\cdot (3h^2)/(16)\cdot (dh)/(dt)`

`(dV)/(dt)=(h^2\pi)/(16)\cdot (dh)/(dt)`

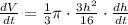
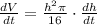
Now we will substitute
`h=300` and
`(dV)/(dt)=-250`

`-250=((300)^2\pi)/(16)\cdot (dh)/(dt)`

`-250=(90000\pi)/(16)\cdot (dh)/(dt)`

`-250\cdot (16)/(90000\pi)=(90000\pi)/(16)\cdot (16)/(90000\pi)\cdot (dh)/(dt)`

`-(4000)/(90000\pi)=(dh)/(dt)`

`-(4)/(90\pi)=(dh)/(dt)`

`(dh)/(dt)=-(4)/(90\pi)`

`(dh)/(dt)=-0.0141471060526129`

`(dh)/(dt)=-0.0141`

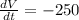
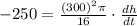
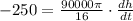
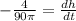
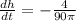
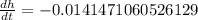
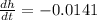
Therefore, the height of the water in the tank is decreasing at a rate of
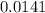`0.0141` cm per hour.