Question

A vending machine is designed to dispense a mean of 7.6 oz of coffee into an​ 8-oz cup. If the standard deviation of the amount of coffee dispensed is 0.3 oz and the amount is normally​ distributed, find the percent of times the machine will dispense less than 7.57 oz.

Answer 1

46.02%

Explanation:

We have been given that a vending machine is designed to dispense a mean of 7.6 oz of coffee into an​ 8-oz cup. The standard deviation of the amount of coffee dispensed is 0.3 oz and the amount is normally​ distributed.

We are asked to find the percent of times the machine will dispense less than 7.57 oz.

First of all, we will find the z-score corresponding to 7.57 using z-score formula.

`z=(x-\mu)/(\sigma)`, where,

z = z-score,

x = Random sample score,

`\mu`= Mean,

`\sigma` = Standard deviation.

`z=(7.57-7.6)/(0.3)`

`z=(-0.03)/(0.3)`

`z=-0.1`

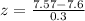
Now we will use normal distribution table to find the probability of z-score less than -0.1 that is
`P(z<-0.1)`

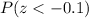
Using normal distribution table we will get:

`P(z<-0.1)=0.46017`

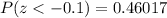
Let us convert
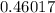`0.46017` into percentage as:

`0.46017* 100\%=46.017\%\approx 46.02\%`

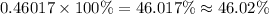
Therefore, 46.02% of times the machine will dispense less than 7.57 oz.