Question

A jury list contains the names of all individuals who may be called for jury duty. The percentage of the available jurors on the list who are women is 53%. Of the 40 people selected to serve as the jury, 27 were women. a. Is there statistically significance evidence suggesting that the proportion of women on the jury differs than the population for jury selection, or could this outcome be explained by chance? Assume that significance level of 0.05. Use the hypothesis testing template provided. b. Based on your conclusion in part A, what type error are you at risk of making? c. Explain what the type of error from part B means in the context of this problem.

Answer 1

a) There is no statistically significant evidence that the proportion of women on the jury differs than the population for jury selection. The outcome can be explained by chance.

b) Type II error

c) This error happens when the claim that the proportion of women on the jury differs from the populations proportion is true, but the evidence is not enough at this level of significance to prove it.

Explanation:

We have a test of hypothesis over a proportion.

The null and alternative hypothesis are:

`H_0: \pi=0.53\\\\H_a: \pi\\eq0.53`

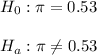
The significance level for this two-tails test is 0.05.

The sample proportion is

`p=X/N=27/40=0.675`

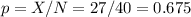
The standard deviation is estimated as:

`\sigma_p=\sqrt{(\pi(1-\pi))/(N)}=\sqrt{(0.53*0.47)/(40)}=0.079`

Then, the z-statistic can be calculated as:

`z=(p-\pi-0.5/N)/(\sigma_p)=(0.675-0.530-0.0125)/(0.079)=(0.1325)/(0.079)= 1.677`

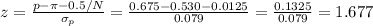
The P-value for z=1.677 is

`P-value=2*P(z>1.677)=0.09354`

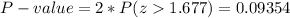
The P-value is larger than the significance level. The null hypothesis is failed to be rejected. There is no statistically significant evidence that the proportion of women on the jury differs than the population for jury selection. The outcome can be explained by chance.

b) As we failed to reject the null hypothesis, the error we are at risk of making is failing to reject a null hypothesis that is false (Type II).

C) In the context of this problem, that would mean that the alternative hypothesis is true and we failed to prove that claim (rejecting the null hypothesis).

This error happens when the claim that the proportion of women on the jury differs from the populations proportion is true, but the evidence is not enough at this level of significance to prove it.