Answer:
(a) k =
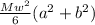
(b) τ =
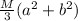 ∝
∝
Step-by-step explanation:
The moment of parallel pipe rotating about it's axis is given by the formula;
I =
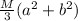 ---------------------------------1
---------------------------------1
(a) The kinetic energy of a parallel pipe is also given as;
k =
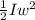 --------------------------------2
--------------------------------2
Putting equation 1 into equation 2, we have;
k =
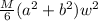
k =
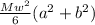
(b) The angular momentum is given by the formula;
τ = Iw -----------------------3
Putting equation 1 into equation 3, we have
τ =
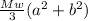
But
τ = dτ/dt =
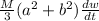 ------------------4
------------------4
where
dw/dt = angular acceleration =∝
Equation 4 becomes;
τ =
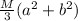 ∝
∝