Question

We are standing on the top of a 1024 foot tall building and launch a small object upward. The object's vertical altitude, measured in feet, after t seconds is h(t)=−16t2+192t+1024. What is the highest altitude that the object reaches?

Answer 1

The height of the object, (measured in feet) t seconds after we threw it is h = -16t^2+160t+

Explanation:

Not only that, the parabola will open downward because of the negative ... So we will find out when the object reaches the highest point by finding the ... (If you need to find out how high this highest point is you would substitute in a 5

One way to find the vertex of a parabola is to complete the square and transform the equation into vertex form

Answer 2

The highest altitude of that object is 1,600 feet.

Explanation:

Given that,

`h(t) = -16t^2+192 t+1024`

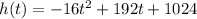
where h(t) is the height of the object after t seconds.

`h(t) = -16t^2+192 t+1024`

Differentiating with respect to t

h'(t)= -32t+192

Again differentiating with respect to t

h''(t)= -32

To find the maximum or minimum value, first we set h'(t)=0.Then we get a equation of t and solve it. Assume t=a is the solution of the equation .

Now check h''(t) at t=a, if h''(a)<0 then the function h(t) has a maximum value at t=a

If h''(a)>0 then the function h(t) has a minimum value at t=a.

Now,

-32t+192=0

⇒32t=192

`\Rightarrow t=(192)/(32)`

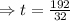
⇒t= 6

h''(6) = -32<0, So the object reaches at its highest altitude after 6 seconds.

Now plunging t=6 in the given function

h(6)= -16 (6)²+192×6 +1024

=1600 feet

The highest altitude of that object is 1,600 feet.