Question

g find all the values of p for which the following functions are improperly integrable on the indicated domain. be sure to prove your claims, ie show that it is improperly integrable for those numbers p, but is not for other numbers 1.f(x)=1/x^p on i =(0,1) 2. f(x) = 1/(x(lnx)^p) on I = (e,inf)

Answer 1

1. In order to make the integral improper
`p` must be 1.

2. In order to make the integral improper
`p` must be 1.

Explanation:

Using the rules of integration we get that for

`f(x)= (1)/(x^p)`

`\int\limits_(0)^(1) (1)/(x^p) \, dx = (x^(1-p))/((1-p)) \, |\limits_(0)^(1) = (1)/(1-p) - 0 = (1)/(1-p)`

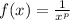
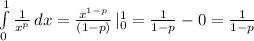
Therefore in order to make that integral improper
`p` must be 1.

If p = 1 then you would have a 1/0 indeterminate form.

2. Using the of integration, specifically substitution we get that for

`f(x) = (1)/(x(ln(x)^p))`

`\int\limits_(e)^(\infty) (1)/(x(ln(x))^p) \, dx = ((ln(x))^(1-p))/(1-p) \, |\limits_(e)^(\infty)`

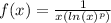
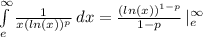
For
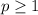`p \geq 1` we would have

`\int\limits_(e)^(\infty) (1)/(x(ln(x))^p) \, dx = (1)/(p-1)`

And the problem is the same. If
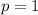`p=1` we would have a 1/0 indeterminate form.