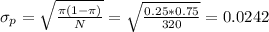Question

A simple random sample of 320 adults was asked their favorite ice cream flavor. Of the 320 individuals surveyed, 30% responded that they preferred mint chocolate chip. At the 0.05 significance level (α=0.05), test the claim that 25% of adults prefer mint chocolate chip ice cream. The mean of the sampling distribution of the sample proportion (assuming the null hypothesis is true) is equal to 0.25. What is the standard deviation of the sampling distribution of the sample proportion (assuming the null hypothesis is true)?

Answer 1

The null hypothesis is rejected. There is evidence that the proportion of adults who prefer mint chocolate chip ice cream differs from 25%.

The mean of the sampling distribution of the sample proportion is 0.25 and the standard deviation is 0.0242 (assuming the null hypothesis is true).

Explanation:

We have the null and alternative hypothesis

`H_0: \pi=0.25\\\\H_a:\pi\\eq 0.25`

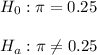
The level of significance is
`\alpha=0.05`.

The sample mean is
`p=0.3`

The standard deviation is estimated as:

`\sigma_p=\sqrt{(\pi(1-\pi))/(N)}=\sqrt{(0.25*0.75)/(320)}=0.0242`

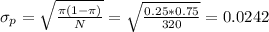
Then, the z-statistic can be calculated as:

`z=(p-\pi-0.5/N)/(\sigma_p) =(0.3-0.25+0.00)/(0.0242) =(0.05)/(0.0242) \\\\z=2.07`

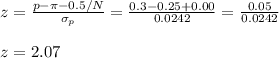
The P-value for this z=2.07 is

`P-value=2*P(z>2.07)=0.04`

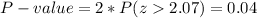
As the P-value is smallet than the significance level, the null hypothesis is rejected. There is evidence that the proportion of adults who prefer mint chocolate chip ice cream differs from 25%.

The sampling distribution will have a mean proportion equal to the population proportion (0.25), as it is not biased.

The standard deviation is calculated as before, and equals 0.0242.

`\sigma_p=\sqrt{(\pi(1-\pi))/(N)}=\sqrt{(0.25*0.75)/(320)}=0.0242`