Question

Suppose that a study of elementary school students reports that the mean age at which children begin reading is 5.4 years with a standard deviation of 0.7 years. Step 1 of 2: If a sampling distribution is created using samples of the ages at which 37 children begin reading, what would be the mean of the sampling distribution of sample means? Round to two decimal places, if necessary.

Answer 1

By the Central Limit Theorem, the mean of the sampling distribution of sample means would be 5.4 years.

Explanation:

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

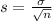For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

In this problem, we have that:

The mean for the entire population is 5.4 years.

So, by the Central Limit Theorem, the mean of the sampling distribution of sample means would be 5.4 years.