Question

Brian's Automotive orders 907 gallon-sized jugs of Mobil 1 5W-40 motor oil per year. Each order has a flat cost of $17 per order and the annual holding cost has been calculated to be $1.82 per jug. They hold no safety stock. What is the optimal total annual cost when ordering based on the EOQ?

Answer 1

The optimal total annual cost is ≈ $1274

Step-by-step explanation:

Given:

• Demand (D): 907
• Holding cost (C): $1.82 per jug
• Ordering cost (O) : $17 per order

To find the optimal total annual cost when ordering based on the EOQ, we use the following formula to find the EOQ:

• EOQ =
  `\sqrt{ (2* D* O)/(C)}`

=
`\sqrt{ (2* 907* 17)/(1.82)}`

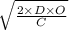
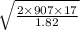
= $130.16

=> annual holding cost (H): 4*EOQ / 2 = 4*130.16 /2 = $260.33

=> annual ordering cost (S) : O*D/EOQ = 1.82*907/130.16 = $12.6

So the optimal total annual cost is:

• D*EOQ / S + EOQ*H/2

= 907*$130.16 / $260.33 + $130.16*$12.6/2

≈ $1274