Question

In a study of government financial aid for college​ students, it becomes necessary to estimate the percentage of​ full-time college students who earn a​ bachelor's degree in four years or less. Find the sample size needed to estimate that percentage. Use a 0.02 margin of error and use a confidence level of 95​%. Complete parts​ (a) through​ (c) below.

a. Assume that nothing is known about the percentage to be estimated.
n=_______
b. Assume prior studies have shown that about 55​% of​ full-time students earn​ bachelor's degrees in four years or less.
n=

Does the added knowledge in part​ (b) have much of an effect on the sample​ size?

A. Yes, using the additional survey information from part​ (b) dramatically reduces the sample size.
B. No, using the additional survey information from part​ (b) only slightly reduces the sample size.
C. No, using the additional survey information from part​ (b) does not change the sample size.
D. Yes, using the additional survey information from part​ (b) only slightly increases the sample size.

Answer 1

a. n=2401 students

b. n=2377 students

c. B. No, using the additional survey information from part​ (b) only slightly reduces the sample size.

Explanation:

a. The sample size for a sample proportion about the mean is calculated using the formula:

`n=((z_(\alpha/2))/(E))^2p(1-p)`

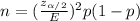
Where p is the proportion and E is the margin of error.

-If nothing is known about the proportion to be studied, we use p=0.5:

`n=((z_(\alpha/2))/(E))^2p(1-p)\\\\=(1.96/0.02)^20.5(1-0.5)\\\\=2401`

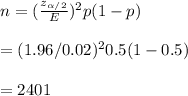
Hence, the required sample size is 2401

b. If the proportion to be estimated is given, we substitute it for p in the formula.

-Given p=0.55, the required sample size can be calculated as:

`n=((z_(\alpha/2))/(E))^2p(1-p)\\\\=(1.96/0.02)^20.55(1-0.55)\\\\=2376.99\approx2377`

Hence, the required sample size for a given proportion of 55% is approximately 2377 students

c. The added information in b had a reducing effect on the sample size:

`\bigtriangleup n=n_a-n_b\\\\=2401-2377\\\\=24`

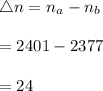
-The sample size slightly reduces by 24 students.

Hence, No, using the additional survey information from part​ (b) only slightly reduces the sample size.