Question

According to the Public Health Service (PHS), the optimal concentration of fluoride in public water supplies is 0.70 mg/L. Suppose that Alicia is an environmental scientist who is testing the quality of tap water a small city, and she believes that officials are adding too much fluoride to the water supply. Alicia tests the water from 60 randomly selected residences and finds that the mean fluoride concentration is 0.79 mg/L, with a standard deviation of 0.36 mg/L. Her data look normally distributed, so she decides to perform a t -test t-test to determine if the mean fluoride level is significantly higher than the PHS recommendation. She chooses a significance level of 0.01. Alicia calculates the one-sample t -statistic t-statistic to be 1.94, which results in a P -value P-value of 0.03. What should Alicia conclude based on her t -test t-test result

Answer 1

Alicia conclude that the mean fluoride level is less than or equal to the PHS recommendation.

Explanation:

We are given that the Public Health Service (PHS), the optimal concentration of fluoride in public water supplies is 0.70 mg/L.

Alicia tests the water from 60 randomly selected residences and finds that the mean fluoride concentration is 0.79 mg/L, with a standard deviation of 0.36 mg/L.

Let
`\mu` = population mean fluoride level

SO, Null Hypothesis,
`H_0` :
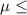`\mu \leq` 0.70 mg/L {means that the mean fluoride level is less than or equal to the PHS recommendation}

Alternate Hypothesis,
`H_a` :
`\mu` > 0.70 mg/L {means that the mean fluoride level is significantly higher than the PHS recommendation}

The test statistics that will be used here is One-sample t test statistics because we don't know about the population standard deviation;

T.S. =
`\frac{\bar X -\mu}{{(s)/(√(n) ) } }` ~
`t_n_-_1`

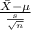where,
`\bar X` = sample mean fluoride concentration = 0.79 mg/L

s = sample standard deviation = 0.36 mg/L

n = sample of residences = 60

So, test statistics =
`\frac{0.79-0.70}{{(0.36)/(√(60) ) } }` ~
`t_5_9`

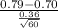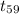
= 1.94

P-value of the test statistics is given to us as 0.03.

The decision rule based on p-value is given by;

• If the P-value of test statistics is more than the level of significance, then we will not reject our null hypothesis as it will not fall in the rejection region.

• If the P-value of test statistics is less than the level of significance, then we will reject our null hypothesis as it will fall in the rejection region.

Now, here the P-value is 0.03 which is clearly higher than the level of significance of 0.01, so we will not reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the mean fluoride level is less than or equal to the PHS recommendation.