Question

The center of mass of a pitched baseball or radius 2.42 cm moves at 23.3 m/s. The ball spins about an axis through its center of mass with an angular speed of 158 rad/s. Calculate the ratio of the rotational energy to the translational kinetic energy. Treat the ball as a uniform sphere.

Answer 1

To solve the problem, it will be necessary to define the rotational and translational kinetic energy in order to determine the relationship between the two. Rotational energy is defined as,

`KE_(Rotational) = (1)/(2) I\omega^2`

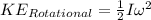
Here,

I = Moment of Inertia

`\omega` = Angular velocity

Now the translational energy will be,

`KE_(Translational) = (1)/(2) mv^2`

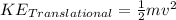
Here,

m = Mass

v = Velocity

Therefore the relation between them will be,

`(KE_(Rotational) )/(KE_(Translational)) = ((1)/(2) I\omega^2 )/((1)/(2) mv^2 )`

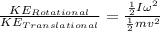
Applying the moment of inertia of a sphere we have,

`(KE_(Rotational) )/(KE_(Translational)) = ((1)/(2) ((2)/(5)mr^2)\omega^2 )/((1)/(2) mv^2 )`

`(KE_(Rotational) )/(KE_(Translational)) = (2)/(5) (r^2\omega^2)/(v^2)`

`(KE_(Rotational) )/(KE_(Translational)) = (2)/(5) ((2.42*10^(-2))^2(158)^2)/(23.3^2)`

`(KE_(Rotational) )/(KE_(Translational)) = 0.01077`

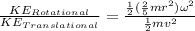
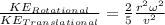
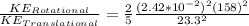
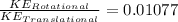
Therefore the ratio will be 0.01077