Answer:
the small mass will drop 11.65 cm below before come to rest
Step-by-step explanation:
Given that:
the mass of the block (M) = 1.40 kg
the inclined angle θ = 25°
spring constant (k) = 30.0 N/m
suspended mass from the block (m) = 40.0 g = 0.040 kg
downward speed (v) = 1.20 m/s
The tension acting vertical on the inclined plane can be expressed as:

For the smaller mass (m)

If we equate equation (1) and (2) together; we have:
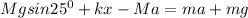
making acceleration (a) the subject of the formula ; we have:

From the third equation of motion

Replacing a with
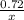 in equation (3); we have:
in equation (3); we have:
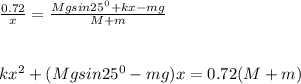
From the equation above; let's substitute our given values;
Then. we have :

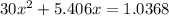
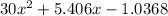 = 0
= 0
Using quadratic formula:
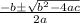
where: a = 30 ; b = 5.406 ; c = -1.0368
Then;
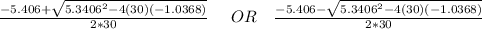
= 0.1165 OR - 0.2967
The distance of how far it drops much be positive; so taking into account of the positive integer; x = 0.1165 m
x= 11.65 cm
Therefore; the small mass will drop 11.65 cm below before come to rest