Answer:
We are given:
n = 100
x(number of heads) = 65
Let's take P= propoortion of head
a) •for null hypothesis:
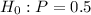
For alternative hypothesis:
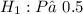
Since it's a 2 tailed test, we have:
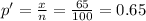
For z-statistic:
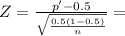

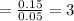
For P value:
2P(z>3) = 2*0.0013
= 0.0026
•As P value (0.0026) is less than level of significance (0.5), we reject the null hypothesis.
b) we are given:
P( fair coins) = 0.999
P(coins not fair) = 0.001
P(head| fair coins) = 0.5
P(head| coins not fair) = 0.65
P(coin weighted|head) will be:
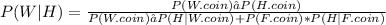
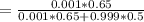
= 0.0013
c) Comparing the conclusions of part (a) and (b) under the hypothesis test we see that they yielded different results.
Using Bayes' theorem, we can see that the probability of the coin being unfair is very unlikely (less) but the null hypothesis tells us otherwise.
The different conclusions gotten are due to methods used or different confidence level.