Question

An astronaut, whose mission is to go where no one has gone before, lands on a spherical planet in a distant galaxy. As she stands on the surface of the planet, she releases a small rock from rest and finds that it takes the rock 0.540 s to fall 1.90 m. If the radius of the planet is 8.60×107 m, what is the mass of the planet?

Answer 1

The mass of the planet is
`M_(planet) =` 144.5 ×
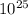`10^(25)` kg

Step-by-step explanation:

We know that g for the planet is given by

`g = G (M_(planet) )/(r^(2) )`

`M_(planet) = (gr^(2) )/(G)` --------- (1)

Acceleration is given by

`a = (2(y_2-y_1))/(t^(2) )`

`a = (2(1.90))/(0.54^(2) )`

`a = g = 13.03 (m)/(s^(2) )`

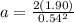
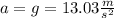
Radius of the planet R = 8.6 ×
`10^(7)` meter

Now put the value of g & R in equation (1)

`M_(planet) = ((13.03)(8.6)^(2)(10^(14) ) )/(6.67 (10^(-11) ))`

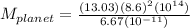
`M_(planet) =` 144.5 ×
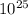`10^(25)` kg

Therefore the mass of the planet is
`M_(planet) =` 144.5 ×
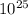`10^(25)` kg