Answer:
(a) $1,020 or more = 0.2358
(b) Between $880 and $1,130 = 0.7389
(c) Between $830 and $940 = 0.3524
(d) Less than $770 = 0.0294
Explanation:
We are given that According to M/PF Research, Inc. report, the average cost of renting an apartment in Minneapolis is $951.
Suppose that the standard deviation of the cost of renting an apartment in Minneapolis is $96 and that apartment rents in Minneapolis are normally distributed.
Let X = apartment rents in Minneapolis
So, X ~ Normal(
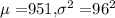 )
)
The z score probability distribution for normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = average cost of renting an apartment = $951
= average cost of renting an apartment = $951
 = standard deviation = $96
= standard deviation = $96
(a) Probability that the price is $1,020 or more is given by = P(X
 $1,020)
$1,020)
P(X
 $1,020) = P(
$1,020) = P(


 ) = P(Z
) = P(Z
 0.72) = 1 - P(Z < 0.72)
0.72) = 1 - P(Z < 0.72)
= 1 - 0.76424 = 0.2358
The above probability is calculated by looking at the value of x = 0.72 in the z table which gives an area of 0.76424.
(b) Probability that the price is between $880 and $1,130 is given by = P($880 < X < $1,130) = P(X < $1,130) - P(X
 880)
880)
P(X < $1,130) = P(
 <
<
 ) = P(Z < 1.86) = 0.96856
) = P(Z < 1.86) = 0.96856
P(X
 $880) = P(
$880) = P(


 ) = P(Z
) = P(Z
 -0.74) = 1 - P(Z < 0.74)
-0.74) = 1 - P(Z < 0.74)
= 1 - 0.77035 = 0.22965
The above probability is calculated by looking at the value of x = 1.86 and x = 0.74 in the z table which gives an area of 0.96856 and 0.77035 respectively.
Therefore, P($880 < X < $1,130) = 0.96856 - 0.22965 = 0.7389
(c) Probability that the price is between $830 and $940 is given by = P($830 < X < $940) = P(X < $940) - P(X
 830)
830)
P(X < $940) = P(
 <
<
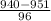 ) = P(Z < -0.11) = 1 - P(Z
) = P(Z < -0.11) = 1 - P(Z
 0.11)
0.11)
= 1 - 0.5438 = 0.4562
P(X
 $830) = P(
$830) = P(


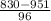 ) = P(Z
) = P(Z
 -1.26) = 1 - P(Z < 1.26)
-1.26) = 1 - P(Z < 1.26)
= 1 - 0.89617 = 0.10383
The above probability is calculated by looking at the value of x = 0.11 and x = 1.26 in the z table which gives an area of 0.5438 and 0.89617 respectively.
Therefore, P($830 < X < $940) = 0.4562 - 0.10383 = 0.3524
(d) Probability that the price is Less than $770 is given by = P(X < $770)
P(X < $770) = P(
 <
<
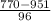 ) = P(Z < -1.89) = 1 - P(Z
) = P(Z < -1.89) = 1 - P(Z
 1.89)
1.89)
= 1 - 0.97062 = 0.0294
The above probability is calculated by looking at the value of x = 1.89 in the z table which gives an area of 0.97062.