Question

Find the area of the figure below.

Answer 1

Answer: ~30.3

Explanation:

The first step is to break the figure into its shapes, this way we can find the individual area of each, then add them together.

We can see that on the left we have a triangle, in the middle a rectangle, and on the right, half of a circle.

The triangle has a height of 4(given). We also know its base is 8, by subtracting the 2 from 10. Now we can solve for the area of the triangle.

A = B x H (1/2)

A = 8 x 4(1/2)

A = 32(1/2)

A = 16

The square has a height of 4(given) and a length of 2(given), so we can solve.

A = B x H

A = 2 x 4

A = 8

The half circle has a diameter of 4(given), so we will solve for the area of the circle then divide by 2.

A = pi(4)

A = ~12.6

A of half circle = 12.6/2

A = ~6.3

Now add the individual areas together to find the area of the complete figure.

6.3 + 8 + 16

30.3

Answer 2

`2\pi` + 24 meters squared

Explanation:

This figure is made up of a trapezoid and a semicircle, so let's find the areas separately then add them up at the end.

The area of a trapezoid is:
`A=((b_1+b_2)h)/(2)` , where b_1 and b_2 are the bases and h is the height.

In this case, b_1 = 2, b_2 = 10, and h = 4. So, we plug these values into the equation to get:
`A=((2+10)*4)/(2) =(12*4)/(2) =(48)/(2) =24`.

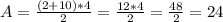Now, we find the area of the semicircle, which is:
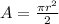`A=(\pi r^2)/(2)` , where r is the radius. Here, the radius is 4/2 = 2. So:
`A=(\pi *2^2)/(2) =(4\pi )/(2) =2\pi`

Now, we add the two together:

24 +
`2\pi`

Thus, the answer is
`2\pi` + 24 meters squared.

Hope this helps!