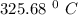Question

A thermistor is placed in a 100 °C environment and its resistance measured as 20,000 Ω. The material constant, β, for this thermistor is 3,650 °C. Find: If the thermistor is then used to measure a particular temperature, and its resistance is measured as 500 Ω, determine the thermistor temperature.

Answer 1

the thermistor temperature =
`325.68 \ ^0 \ C`

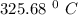
Step-by-step explanation:

Given that:

A thermistor is placed in a 100 °C environment and its resistance measured as 20,000 Ω.

i.e Temperature

`T_1 = 100^0C\\T_1 = (100+273)K\\\\T_1 = 373\ K`

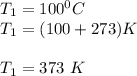
Resistance of the thermistor
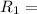`R_1 =` 20,000 ohms

Material constant
`\beta` = 3650

Resistance of the thermistor
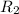`R_2` = 500 ohms

Using the equation :

`R_1 = R_2 \ e^(\beta) ((1)/(T_1)- (1)/(T_2))`

`(R_1)/( R_2) = \ e^(\beta) ((1)/(T_1)- (1)/(T_2))`

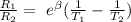
Taking log of both sides

`In \ (R_1)/( R_2) = In \ \ e^(\beta) ((1)/(T_1)- (1)/(T_2))`

`In \ (R_1)/( R_2) = {\beta} ((1)/(T_1)- (1)/(T_2))`

`\frac{ In \ (R_1)/( R_2)}{ {\beta}} = ((1)/(T_1)- (1)/(T_2))`

`(1)/(T_2) = (1)/(T_1) - \frac{ In \ (R_1)/( R_2)}{ {\beta}}`

`{T_2} = (\beta T_1)/(\beta - In ((R_1)/(R_2))T)`

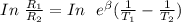
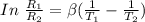
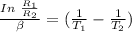
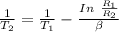
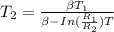
Replacing our values into the above equation :

`{T_2} = (3650*373)/(3650 - In ((20000)/(500))373)`

`{T_2} = (1361450)/(3650 - 3.6888*373)`

`{T_2} = (1361450)/(3650 - 1375.92)`

`{T_2} = (1361450)/(2274.08)`

`{T_2} = 598.68 \ K`

`{T_2} = 325.68 \ ^0 \ C`

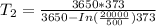
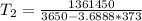
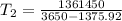
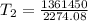
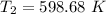
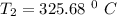
Thus, the thermistor temperature =
`325.68 \ ^0 \ C`