Question

Consider Hilbert’s Grand Hotel, which has countably infinite rooms. Initially the Grand Hotel is empty. But then countably infinitely many busses show up. Bus 1 has 1 guest, Bus 2 has 2 guests, Bus 3 has 3 guests, and so on. (a) Describe how the hotel can accommodate all the guests arriving so that each guest gets their own individual room.

Answer 1

The correct answer is by allotting rooms of nth guest of nth bus to nth power of nth prime numbers.

Explanation:

There are infinite number of rooms in Hilbert's Grand Hotel.

The hotel is empty. Now countably infinitely many buses show up.

Bus 1 has 1 guest, Bus 2 has 2 guests, Bus 3 has 3 guests, and so on.

Thus the hotel accommodates guest of bus 1 to room number 2, the first prime number.

Again the hotel accommodates 2 guests of bus 2 to room number 3 (the next prime number) and
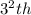`3^(2) th` room.

Again the hotel accommodates 3 guests of bus 3 to room number 5(the next prime number);
`5^(2) th` room; and
`5^(3) th` room.

As there are infinitely many prime numbers, this allocation is feasible and there would be no overlapping rooms.

This way the hotel can accommodate countably infinitely many buses with each guests having individual rooms.