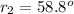Answer:
a
The path of light ray through the glass is shown on the first uploaded image
First surface:
Angle of incidence is
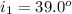
Angle of refraction is

Second surface:
Angle of incidence is
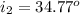
Angle of refraction is

b
Since the angle of incidence is equal to the angle of reflection
Then at the first surface the angle of reflection is
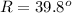
And at the first surface the angle of reflection is
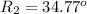
Step-by-step explanation:
From the question we are told that
The angle of incidence is
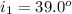
The refractive index of the prism is
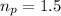
The angle of the prism is
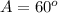
The path of light ray through the glass is shown on the first uploaded image
For the first surface of the prism
According to Snell's law
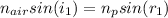
The refractive index of air
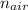 has a constant value of 1
has a constant value of 1
Now making the angle of refraction at the first surface of the prism
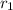 the subject
the subject
![r_1 = sin^(-1)[(sin (i_1) )/(n_(p)) ]](https://img.qammunity.org/2021/formulas/physics/college/ucn0025l7gxdds2basncx39xqp1smcxe3l.png)
![= sin^(-1)[(sin(39.8))/(1.5) ]](https://img.qammunity.org/2021/formulas/physics/college/m737l1unztl4u9fkablrtbfhumozod7sfm.png)

For the second surface of the prism
looking at the diagram on the first uploaded image the angle of incidence is mathematically evaluated as
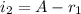
Substituting values
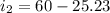

According to Snell's law
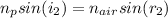
Now making the angle of refraction at the second surface of the prism
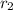 the subject
the subject
![r_2 = sin^(-1) [(n_p sin(i_2))/(n_air) ]](https://img.qammunity.org/2021/formulas/physics/college/c6s4f4dbmam7fe3t4560vtpz5u2h0po436.png)
Substituting values into the equation
![r_2 = sin^(-1) [(1.5 * sin(34.77))/(1)]](https://img.qammunity.org/2021/formulas/physics/college/ep0dimp32l3akdquz6c0yyyyb15nn581b2.png)