Question

At time t=0 a 2150 kg rocket in outer space fires an engine that exerts an increasing force on it in the +x−direction. This force obeys the equation Fx=At2, where t is time, and has a magnitude of 888.93 N when t=1.25 s.

a) What impulse does the engine exert on the rocket during the 4.0 s interval starting 2.00 s after the engine is fired?
b) By how much does the rockets velocity change during this interval?
c) Find the SI value of the constant A, including its units.

Answer 1

Step-by-step explanation:

Given that,

Mass of the rocket, m = 2150 kg

At time t=0 a rocket in outer space fires an engine that exerts an increasing force on it in the +x−direction. The force is given by equation :

`F=At^2`

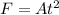
Here F = 888.93 N when t = 1.25 s

(c) We can find the value of A first as :

`F=At^2\\\\A=(F)/(t^2)\\\\A=(888.93)/((1.25)^2)\\\\A=568.91\ N/s^2`

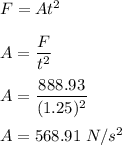
The value of A is
`568.91\ N/s^2`.

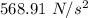(a) Let J is the impulse does the engine exert on the rocket during the 4.0 s interval starting 2.00 s after the engine is fired. It is given in terms of force as :

`J=\int\limits {F{\cdot} dt}`

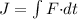
Limits will be from 2 s to 2+ 4 = 6 s

It implies :

`J=\int\limits^6_2 {At^2{\cdot} dt}\\\\J=A\int\limits^6_2 {t^2{\cdot} dt}\\\\J=A(t^3)/(3)|_2^6\\\\J=568.91* (1)/(3)* (6^3-2^3)\\\\J=39444.42\ Ns`

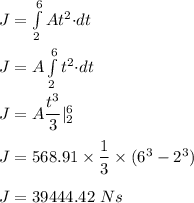
(b) Impulse is also equal to the change in momentum as :

`J=m\Delta v\\\\\Delta v=(J)/(m)\\\\\Delta v=(39444.42)/(2150)\\\\\Delta v=18.34\ m/s`

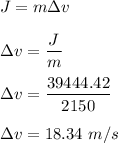
Hence, this is the required solution.